About Applied Mathematics

Applied mathematics is a branch of mathematics that focuses on the application of mathematical theory and methods to other areas such as physics, biology, medicine, computer sciences, life sciences, etc. A central part of applied mathematics is that of Mathematical Modeling, the process through which a real-world problem is transformed into a mathematical problem. For a comprehensive view of applied mathematics, visit the Society for Industrial and Applied Mathematics SIAM Webpage.

Core basic courses in Applied Mathematics include: MTH 303 (Ordinary Differential Equations), MTH 421 (Numerical Analysis I), MTH 422 (Numerical Analysis II), MTH 507 (Introduction to Partial Differential Equations) and MTH 580 (Applied Mathematics). For a brief description of these and other courses see the undergraduate and graduate catalogs.

Applied Mathematics Faculty: Shouchuan Hu, Jorge Rebaza, XingPing Sun, Cameron Wickham, Matthew Wright.

In all applied mathematics-related courses, our students receive not only a rigorous mathematical background on every the topic, but also a wide range of classical and current real-world applications, where the beauty and usefulness of mathematical concepts and methods are highlighted. Seminars are organized where students present to the audience (faculty and students) some of the theory, methods and applications they learned in class.

Here is a partial list of talks presented by MTH 303, MTH 421, MTH 422 and MTH 580 students at various seminars at the Department of Mathematics :

2004

1. A Mathematical Model of Whales and Krills, by Adam Morris.
2. Cell Populations and Dynamical Diseases, by Carla Magee.
3. IS-LM Keynesian Economic Model, by Wilson Forrester.
4. Competition and Hunter Models, by Jennifer Pope.
5. Chaotic Systems and Chua's Circuit, by Dao Tran. Download

2005

1. Multiple Shooting Method for Boundary Value Problems, by Timothy Brown and Peter Hansen. Download
2. Love Dynamics and Chaos, by Elisabeth Farrand. Download
3. Modeling Excitability in Nerve Membranes, by Gayle Green and Justin Ricklefs. Download
4. Matrix Factorizations and Information Retrieval, by Jeremy Chapman, Grant Gelven and Benjamin Lakin. Download
5. HITS: An Eigenvector Numerical Method for Web Information Retrieval, by Larry Philips and John Yankowski. Download
6. PageRank: Google's Vector Space Method for Web Page Ranking, by Nathan Carlisle and Michael McDermott. Download
7. SALSA: A New Eigenvector method for Web Page Ranking, by Adam Simkins. Download
8. Interpolating Data with Cubic Splines, by David Lindell and Lewis Stone. Download

2006

1. Bifurcation to chaos, by Jaeson Day, Jonathan Carter and John Chiles . Download
2. Limit cycles and Hopf bifurcation, by Chris Inabnit, Tom Buck and Brandon Turner. Download
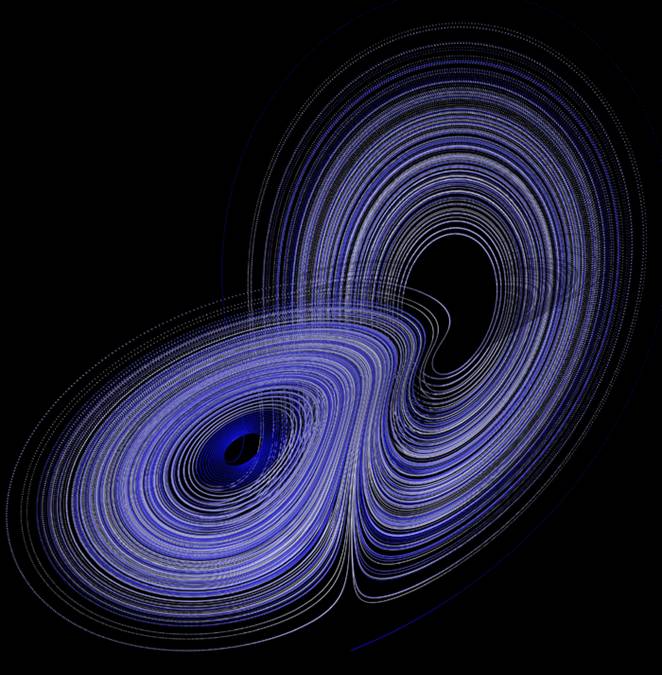
3. Chaos and Lorenz attractor, by Newell Reeser, Regal Ferrulli and Travis Wolf. Download
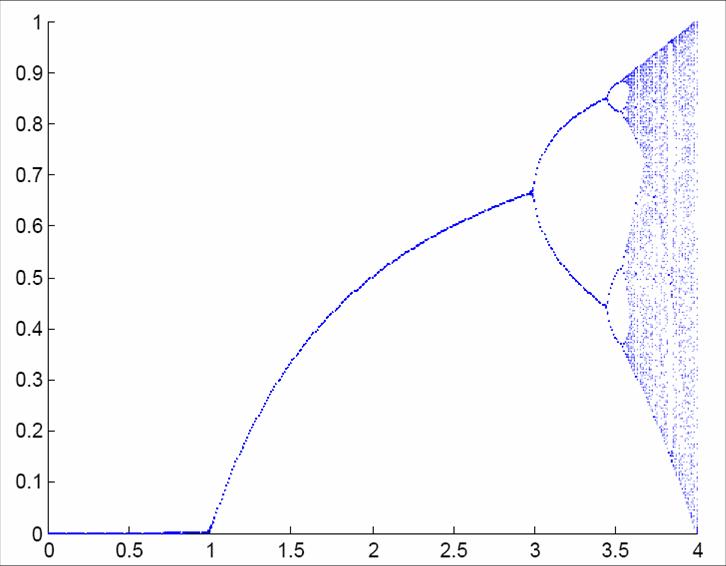
4. Difference equations and period doubling, by Christina Enneking, Kailey Enloe and Nicole Walcutt . Download
5. Bezier Curves and Postcript Fonts, by Ernest Elliot, Christopher Geers, Michael Smith and Tracey Wharton. Download
6. Discrete Cosine Transform and Image Compression, by Thomas Buck, Regal Ferrulli, Zachary Hilty and Jimmie Maggard. Download
7. Multiscale method, by Lauren Garten, Shaun Dunn and Matt Smith.
8. Why do we need multiscale method?, by Ryan Miller.
9. Homogenization, by Evan Kloeppel, Andy Samson and Matt Summer.

2007

1. SVD and Compression, by Annie Johnson . Download
2. SVD and Cryptography, by Nik Clark. Download
3. SVD and Digital Signals, by Tim Sheen. Download
4. Computation of Google's PageRank, by Tom Mangan. Download

 

2008

1. Extrapolation and Romberg's algorithm, by Tom Mangan. Download

2. Adaptive Simpson's rule, by Nicole Typaldos. Download

3. Gaussian quadratures, by Jonathan Carter. Download

4. Cubic spline interpolation and applications, by Mark Coose, Joetta Swift and Micah Weiss. Download

5. Iterative Aggregation and Disaggregation, by Nicole Typaldos. Download

 

2009

1. Computer algebra and pharmacokinetics, by Anna Madras and Steve Parry.

2. Web link matrix permutations, by Aries Chang, Cody Lawson and Michael Dwyer. Download

3. Approximate iterative aggregation, by Jesse Ehlert, Justin Well and Li Zhang. Download

4. The fundamental theorem of linear algebra, by Justin Underwood and Jacob Severs. Download

 

2010

1. Helmoltz equation with applications to cloaking, by Li Zhang. Download, Download_2

2. Maximum explosion pressure of gas-air mixtures, by Katharina Voelkel. Download

 

2011

1. Monte Carlo simulation, by Brett Foster. Download

2. Huffman Coding explained, by Justin Bancroft. Download

3. Dynamics of Leslie-Gower Models, by Jacob Swett and Josh Durham. Download

 

2012

1. Modeling Dynamics of variable species interactions, by Katharina Voelkel. Download

2. Dormand and Prince Approach to implementing adaptive R-K Fehlberg algorithms, by William Mize. Download

3. Schur factorization and applications, by Heath Gemar. Download

4. Krylov subspaces and the adaptive Arnoldi method, by Dustin Rich. Download

 

Cubic spline interpolation	Chaos in nonlinear love triangles
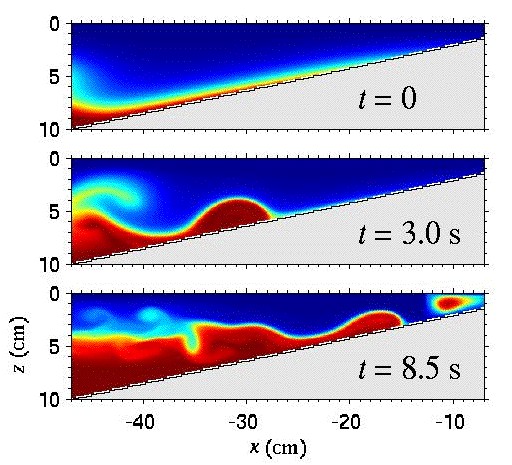
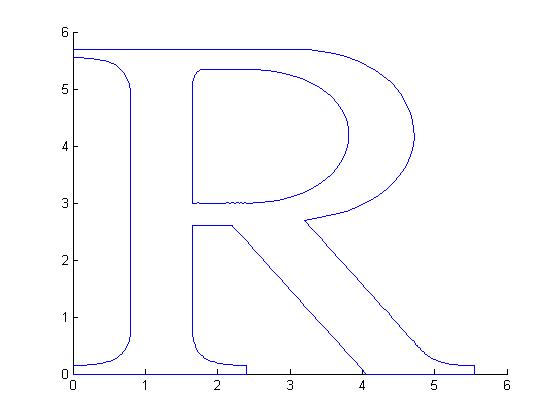
Numerical modeling of ocean waves	T-Roman font using Bezier curves
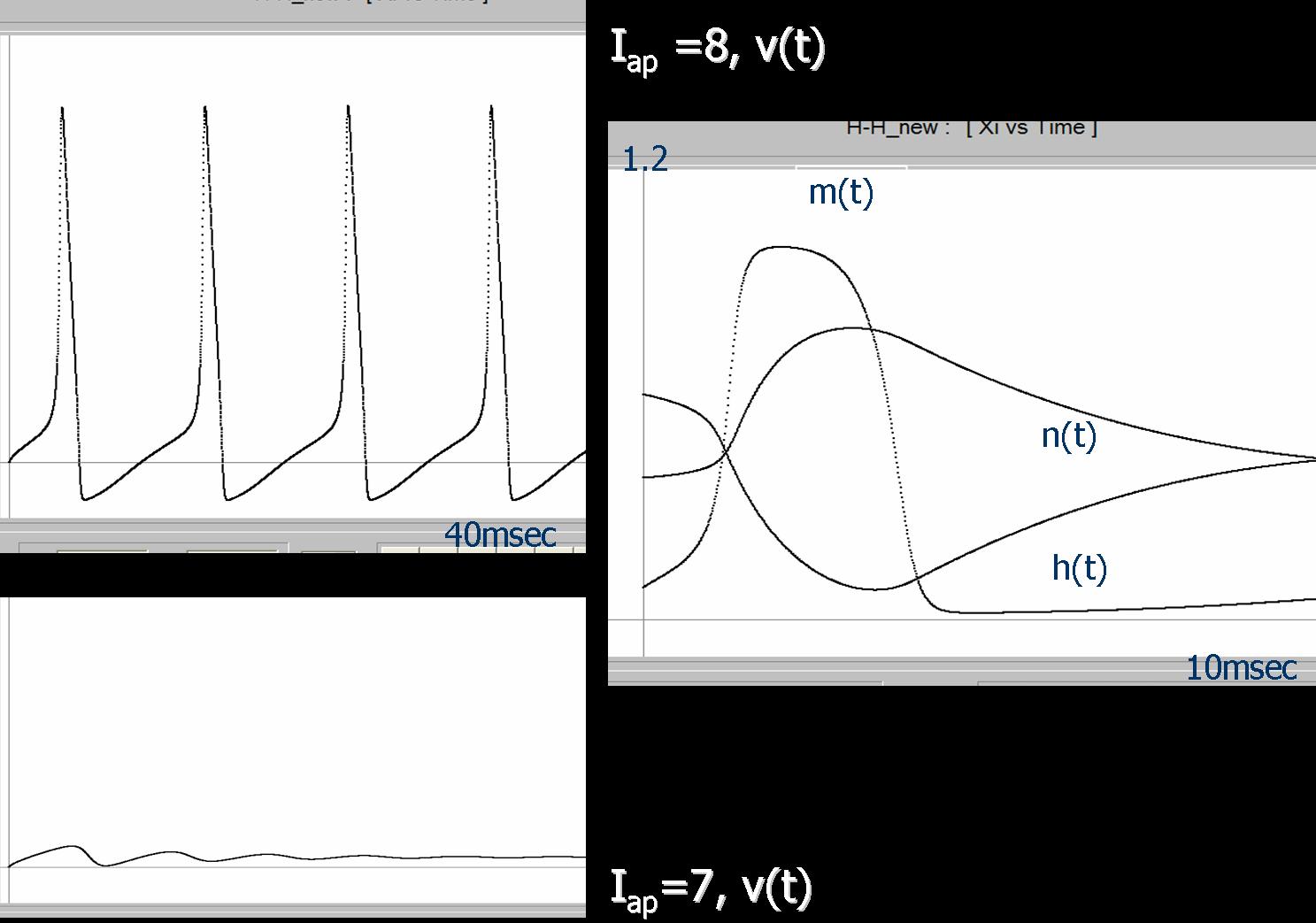
Nerve axon membrane modeling	Compression using discrete cosine transform
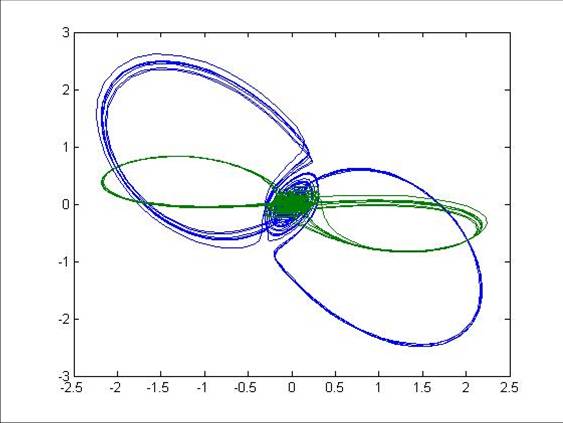
Lorenz' strange attractor	Bifurcation in Logistic map

ANNOUNCEMENT:

The summers of 2012, 2013, 2014, the Department of Mathematics will host NSF-sponsored Research Experiences for Undergraduates (REU) in the areas of Abstract Algebra, Combinatorics and Applied Mathematics for students from Missouri and neighboring states, under the direction of Les Reid, Xingping Sun, and Jorge Rebaza.

For more information, visit our REU Website.